|
Math can be tough, Believe me, I KNOW. But the good thing is that with math, we can show very easily WHERE we stop our understanding.
In class we always talk about how when we read a problem, we can usually take ourselves SO FAR before we become stuck. We NEVER Draw a picture first, we NEVER just dive right in - we start from the beginning. I may not know what to do right now, but there is stuff I can do to start off. I can pull out the information, I can draw a picture to match it, I can write out my thinking. Some things we do in class to trick our brains into remembering what to do:
Look below at steps to solve a problem we did in class. Click each link below to be brought to a youtube video showing the strategy listed.
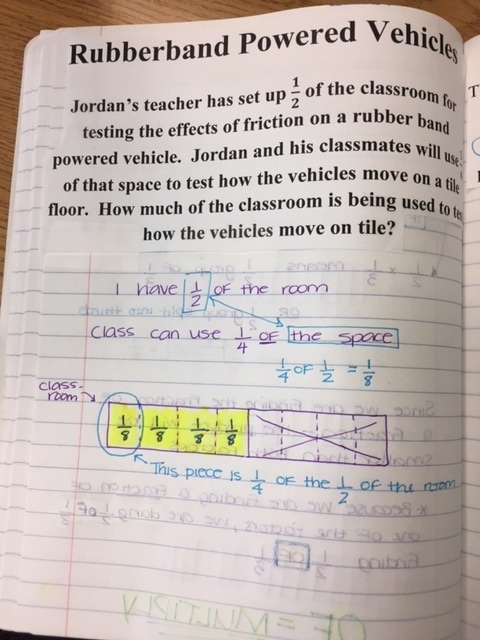
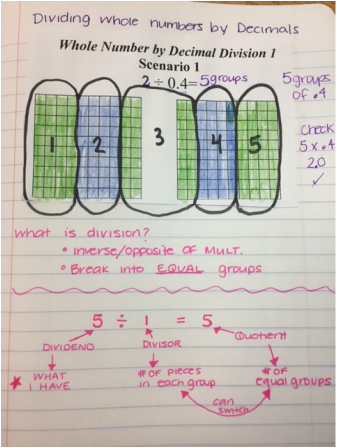
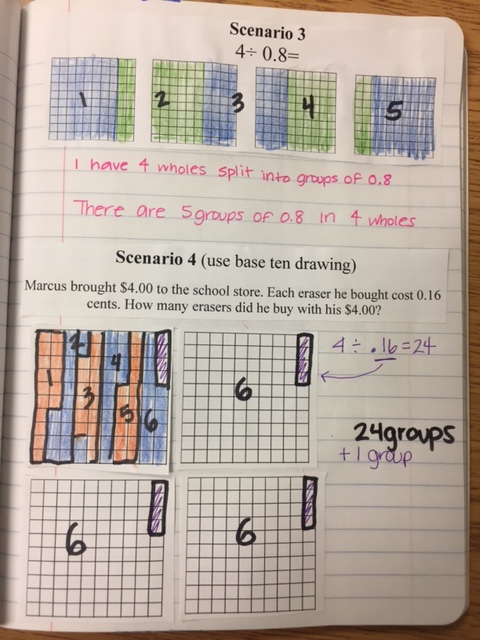
It is NO secret that I am a fan of GRIDS and the AREA MODEL. The Area Model is my jam! In my personal opinion, they are the easiest to understand and very hard to mess up once you get the hang of it. The area model will continue to be used when we do fractions as well and is ALWAYS the most popular strategy. Wake county provides math videos for all the concepts taught, you just have to do a little search :) Below you will see a few different ways to multiply decimals. 1. Since multiplication is just repeated addition, students may use a grid to repeatedly add the same number over and over. Ex: .35 x 3 --- the student would shade .35 two times to show the final product of .70. The first image shows that when we multiply by 10, 100, or 1000 the place value increases or "a zero is added" - However, when we multiply by 0.1, 0.01, .001 - the opposite happens, it is the inverse. When we multiply these numbers we are essentially dividing by 10, 100, and 1000. This is meant to show that when we multiply a number by 1, we get the original number, but when we multiply a number by LESS than 1, we will always get a smaller number. This next image shows the rules of multiplying numbers by 10, 100, 1000 and the inverse decimals and how they compare. This last image shows the Area Model. We use an acronym called *PEACE*
this stands for.. P-problem, E-estimate, A-actual, C-check, E- evaluate P- what is the problem asking us? Write it out E- We estimate to determine what our answer should be around. A- Solve the actual, real answer using a model. C- Check - do a check using the standard algorithm E- evaluate - compare this with your estimate and ask yourself - Does this make sense? If she filled 4.5 ounce bottles, does it make sense that she would use around 15 ounces? Often times when students have a crazy answer, this is where they can catch it. Using these steps helps to avoid what we often refer to as, "Careless mistakes" - when we do ALL of the steps (yes they may seem tedious) - we rarely make mistakes. Skipping steps is when we mess up! MOVING ON... Below is the area model... Area models just break apart the numbers into smaller sections. See the model below. Once they have found each section, they add the partial products together to get the final answer.
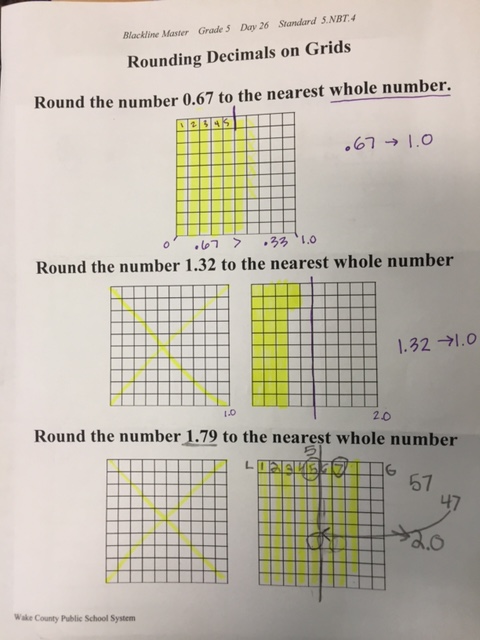
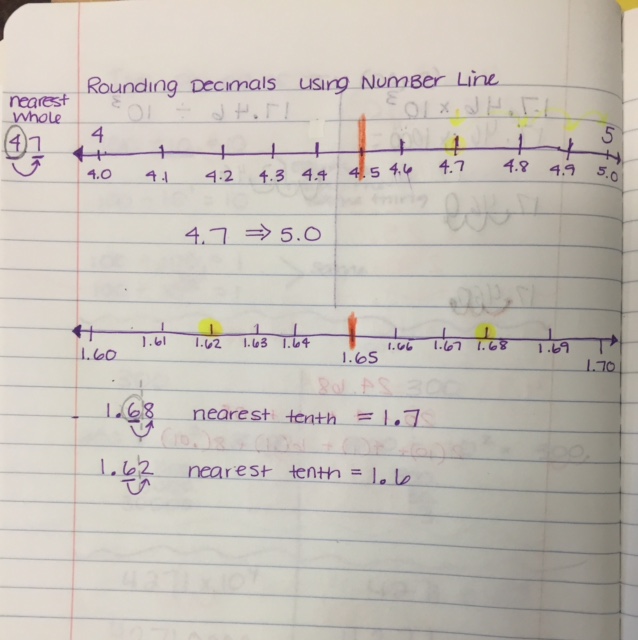
We expanded rounding into number lines. Number lines are the HARDEST to create, but the easiest to see with your eyes!
|
AuthorWrite something about yourself. No need to be fancy, just an overview. Archives
May 2017
Categories |


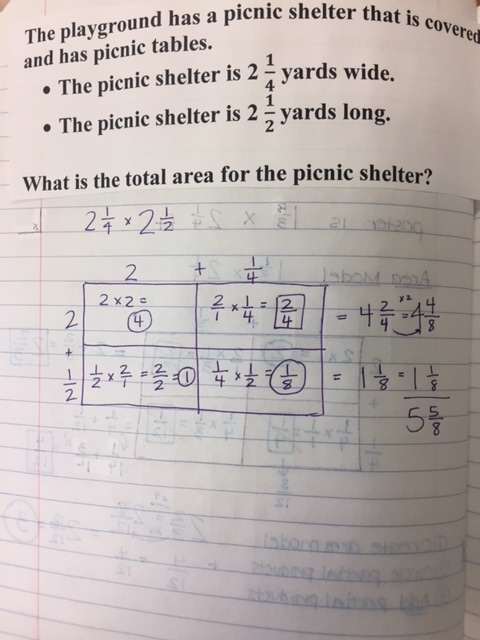



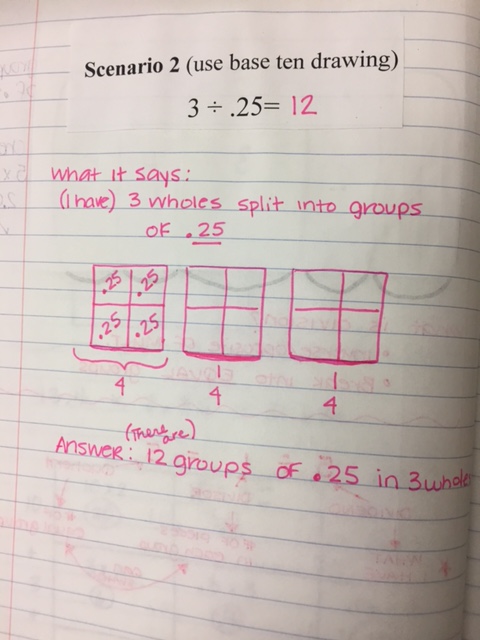
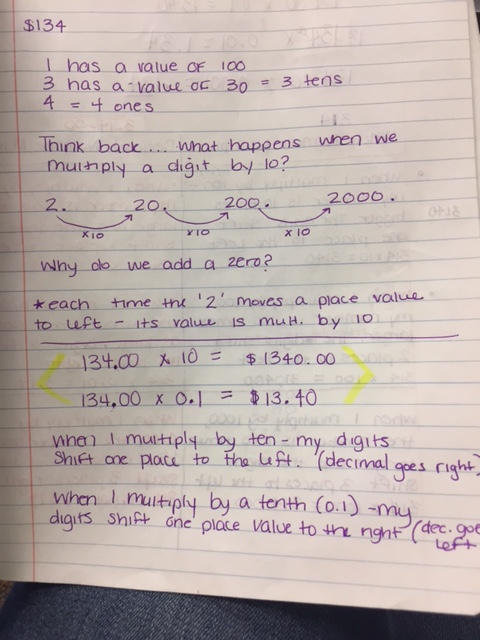

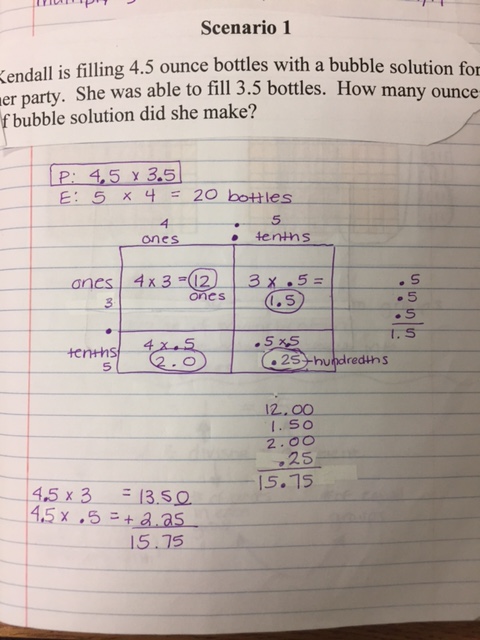
 RSS Feed
RSS Feed
