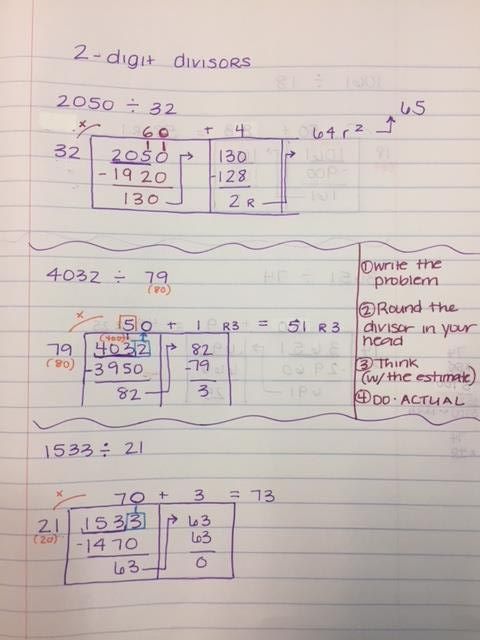
There are classroom notes if you scroll further to the bottom about how to multiply and divide by powers of ten.
|
CLICK HERE FOR HOW TO MULTIPLY AND DIVIDE BY 10 - 100 - 1000
There are classroom notes if you scroll further to the bottom about how to multiply and divide by powers of ten.
0 Comments
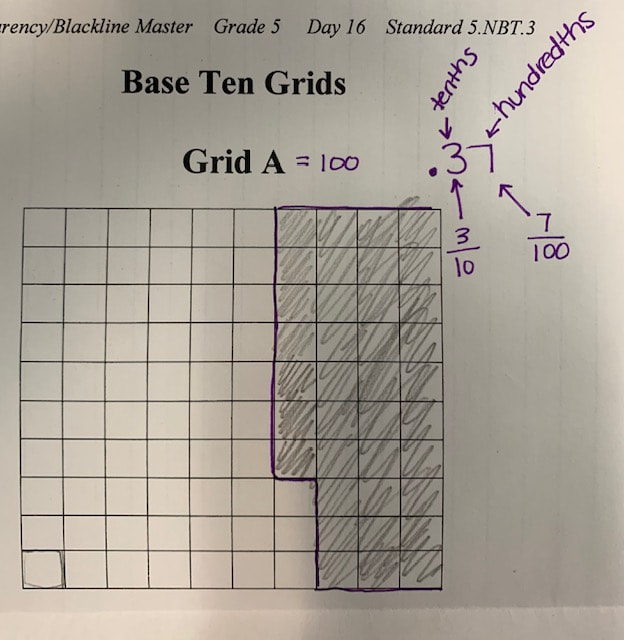
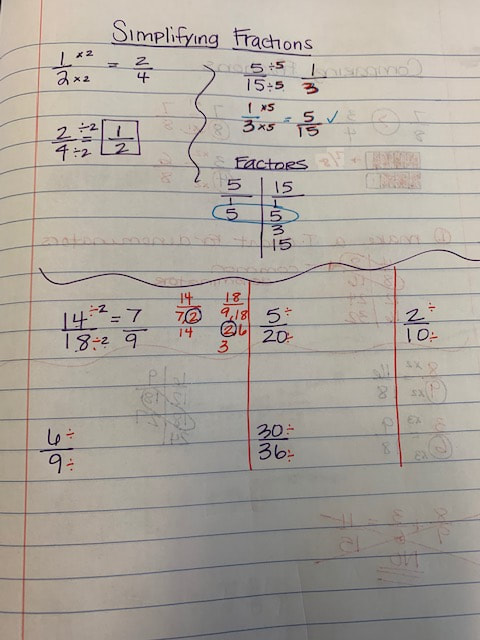
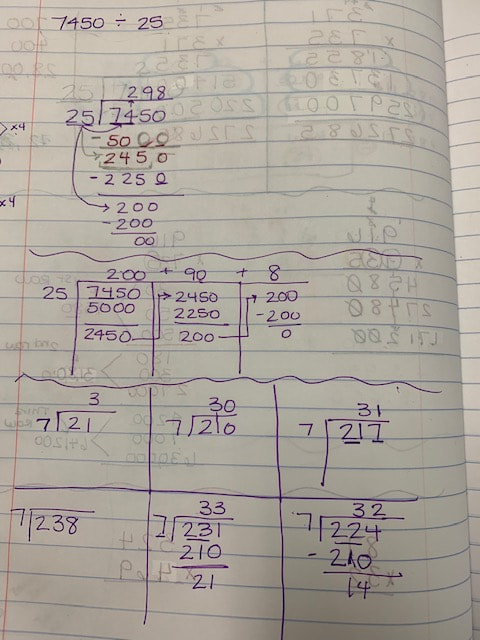
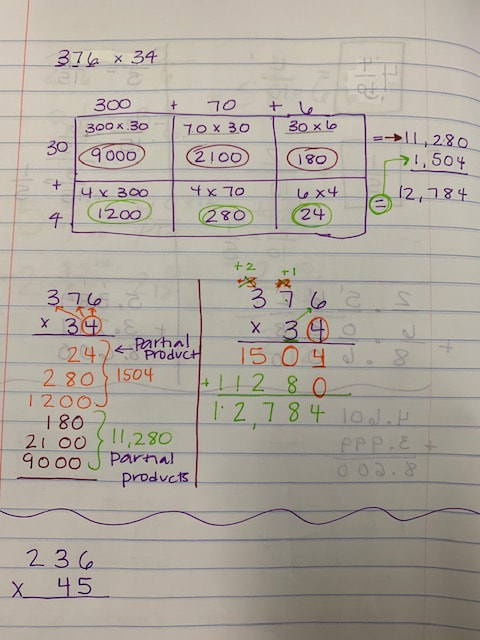
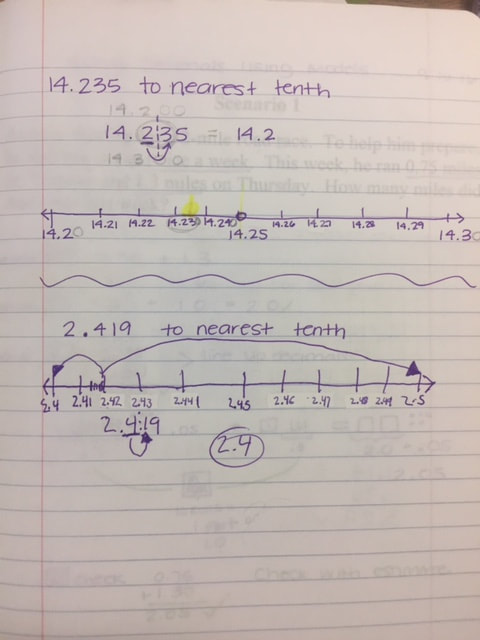
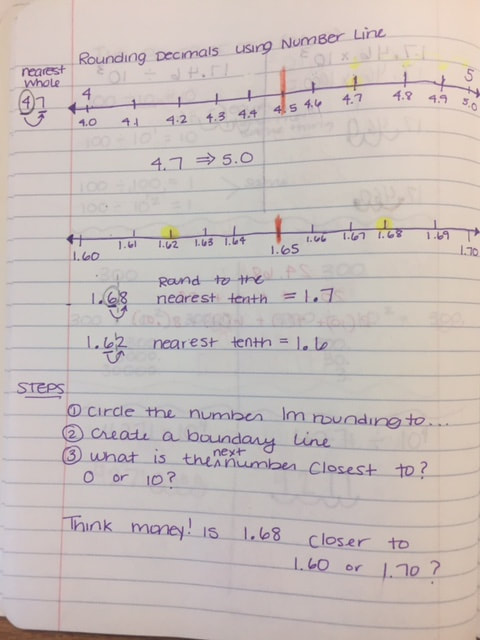
I did not add multiplying decimals lesson one because the images were distorted when I transferred them to my computer. I will try to re do them and post them. Below are the examples from day 2.
|
AuthorWrite something about yourself. No need to be fancy, just an overview. Archives
December 2019
Categories |
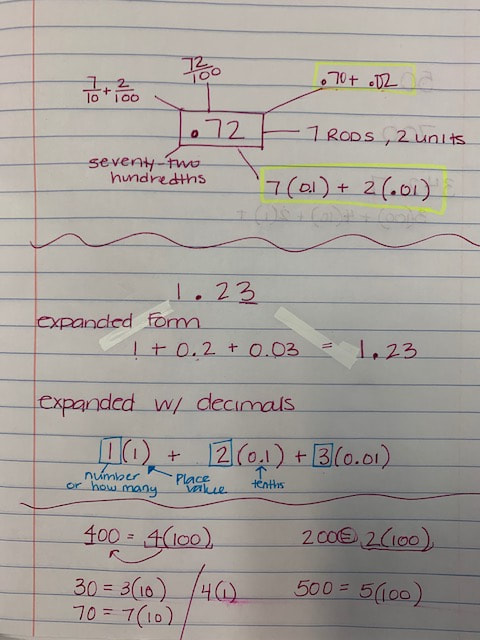



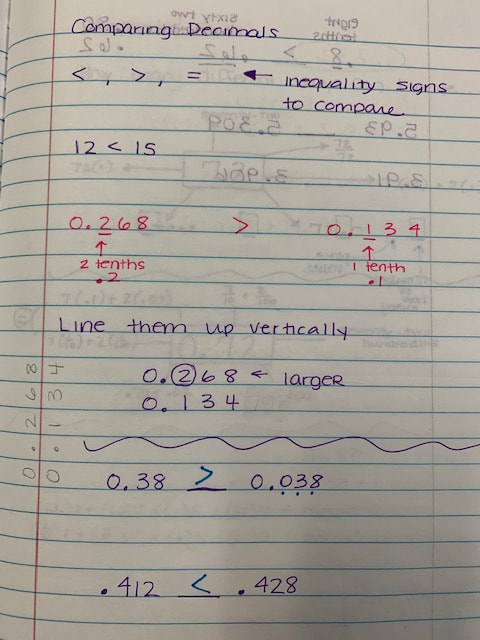

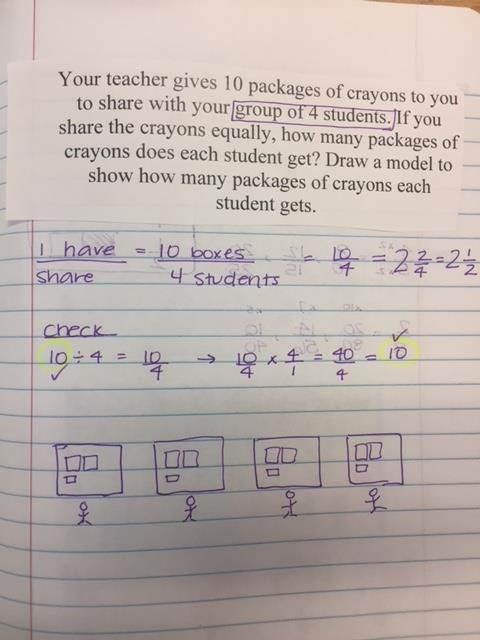


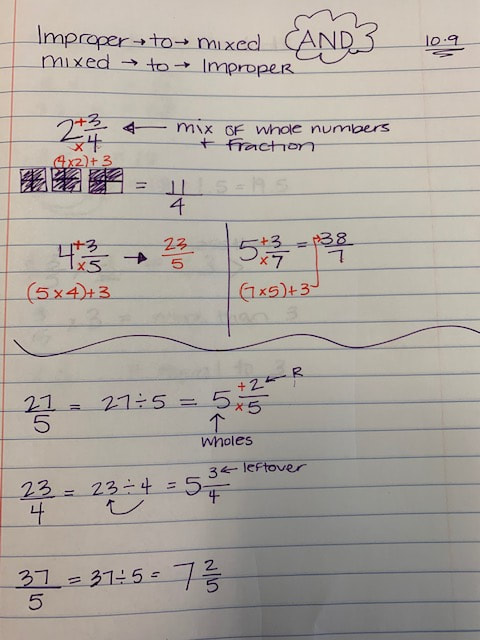









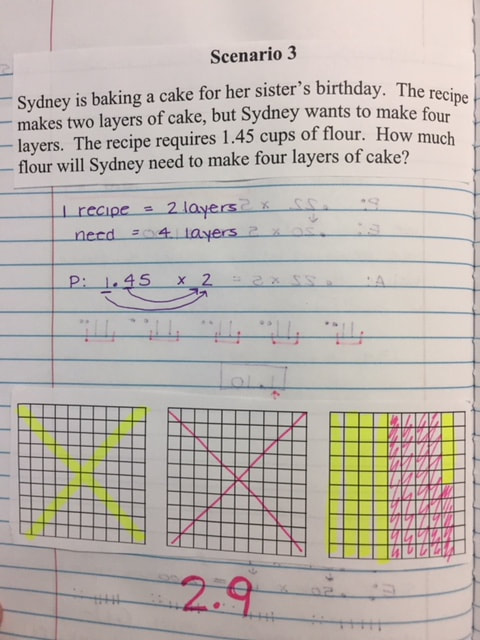
 RSS Feed
RSS Feed
